2025. 4. 28. 22:59ㆍElectronic Warfare/EW Technology
3부에서는 수신되는 펄스 간의 time interval의 의미와 어떻게 ELINT 수신기에서 펄스의 TOA를 알아내는지에 대해 알아본다.
Time Interval Measurements
ELINT 수신기에서 레이다 펄스의 TOA(Time of Arrival)를 측정하는 것은 레이다 수신기가 표적의 거리를 알아내는 것과 유사하다고 할 수 있다.
그러나 아래와 같은 차이점이 있다.
1. 레이다 수신기는 수신된 펄스에 대한 matching 작업을 하지만 ELINT 수신기는 보통 수신된 펄스에 이러한 matching을 하지 않는다.
2. 레이다와는 다르게 일반적으로 단일 펄스의 레이다 거리 지연의 불확실성은 펄스 지속시간 보다 훨씬 작을 필요가 없다. 또한 레이다의 표적 거리는 많은 펄스들의 integration을 기반으로 탐지하지만 ELINT 분석가들은 단일 펄스의 TOA 측정에 있어서 매우 작은 불확실성만이 요구되며 펄스의 상승 시간의 일부분만 필요할 수 있다.
3. 레이다에서 관심을 두는 시간 가격은 펄스를 송신하는 이미 알고있는 시간부터 표적으로부터 반사된 펄스가 수신되는 알지 못하는 시간까지의 간격을 말한다. ELINT에서 관심을 두는 파라미터는 두 펄스 간의 시간이다. 즉, 각 펄스의 시간은 불확실 해도 상관없다.
ELINT 수신기가 레이다 신호에 matching 하지 않는다는 점 때문에 ELINT 수신기의 대역폭은 펄스 지속시간의 역수보다 넓어야 한다.
이것은 활용가능한 SNR을 줄이지만 반면에 시간의 측정에 있어서 펄스의 모양과 송신 펄스의 상승 시간에 대한 제한을 허용가능하게 한다.
또 다른 ELINT의 중요한 요소는 수신되는 신호의 세기가 R-4 대비 R-2 만큼의 전파 장점이 있다는 것이다.
[ Digital Thresholding ]
보통 많이 사용되는 펄스의 TOA 결정 방법은 임계치를 사용하는 것이다.
그러나 고속의 A/D 컨버터가 TOA를 결정하기 위한 다양한 디지털 신호 처리 알고리즘에 널리 사용된다.
여기서 A/D 컨버전 속도인 fs와 양자(quantization) 에러가 TOA 측정 정확도를 결정짓는 중요 요소들이다.
신호를 재형성하는데 요구되는 최소의 컨버전 속도는 비디오 대역폭(또는 신호의 상승 시간)에 의해 결정된다.
임계치 결정 프로세스를 단순하게 하기 위해서는 펄스의 상승 시간 내에서 많은 수의 샘플(h)을 갖는 것이 유리하다.

반면에 펄스의 상승 시간에 따른 많은 수의 샘플들은 A/D 컨버터의 처리 용량을 초과할 수 있다.
샘플링 속도가 비디오 신호 내에서 가장 높은 주파수 보다 두 배 이상 빠르면, 펄스 재구성을 위한 샘플 간의 보간(interpolation)이 사용될 수 있으며 TOA를 찾을 수 있다.
TOA를 측정할 때에 A/D 컨버터의 양자 에러 영향성을 반드시 고려해야 한다.
일반적으로 신호 크기의 비트 수는 신호 대역폭(컨버전 속도)이 증가할수록 줄어든다.
그 이유는 A/D 컨버터가 신호 레벨을 수집하는 동안 샘플링 윈도우는 유한하기 때문이다.
특정 해상도 비트의 수를 갖는 A/D 컨버터의 최대 SNR과 완전한 한 주기의 사인파가 입력된다면 다음과 같이 계산된다.
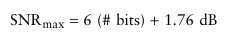
위 식을 보면 주어진 SNR 내에서 A/D 컨버터는 반드시 최소의 해상도 비트수를 가져야 한다는 의미를 알 수 있다.
예를 들면 컨버젼 프로세스 동안 40 dB의 SNR을 유지하기 위해서 A/D 컨버터 해상도는 최소 6.3의 비트수를 가져야 한다.
고속 낮은 해상도의 A/D 컨버터는 디지털 lowpass 필터링 출력을 통해 더 높은 SNR을 얻을 수 있음을 주목할 필요가 있다.
만약 샘플링 속도가 관심 대상이 되는 신호보다 높다면 이 필터링에 의해 잡음이 제거될 수 있다.
SNR의 향상은 다음의 식과 같다.

식에서 볼 수 있듯이 4배의 오버 샘플링은 6 dB의 SNR 개선을 가져올 수 있으며 한 개의 해상도 비트를 추가한 것과 같다.
신호가 디지털 형태라면, 정교한 임계치 기법을 생각해 볼 수 있다.
그러나 고속 해상도의 A/D 컨버터는 고속의 데이터 속도를 제공한다.
예를 들면, 샘플당 8 비트의 1 GHz 샘플링 속도를 갖는 컨버터는 초당 109 바이트를 생성해 낼 수 있다.
이를 위해서는 매우 큰 저장장치가 필요하거나 아니면 저장되는 데이터 양을 줄이기 위해서 실시간의 임계치가 구성되어야 한다.
후자의 경우, 단순한 형태의 임계치 알고리즘만이 가능하다.
만약 계산 자원이 가능하다면, 펄스 중심 위치에 대한 계산은 TOA의 정의로 간주될 수 있다.
신호 크기의 50% 위치에 대한 더욱 정밀한 계산은 많은 다른 기법을 통해 가능하며 그중 하나는 아래와 같다.
1. 펄스의 최대 크기를 찾는다
2. 최대 신호 크기의 50%를 넘는 샘플의 중앙값으로 신호의 크기를 정의
3. 보간을 통해 신호 크기의 50%를 넘는 펄스의 상승 시간을 찾는다.
다음 4부에서는 PRI의 분석하는 기법에 대해 알아본다.
출처 : ELINT - The Interception and Analysis of Radar Signals
'Electronic Warfare > EW Technology' 카테고리의 다른 글
| Pulse Repetition Interval Analysis -(5) (2) | 2025.05.25 |
|---|---|
| Pulse Repetition Interval Analysis - (4) (1) | 2025.05.01 |
| Pulse Repetition Interval Analysis - (2) (1) | 2025.04.27 |
| Pulse Repetition Interval Analysis -(1) (1) | 2025.04.13 |
| Probability of Intercept (0) | 2025.04.04 |