이번에는 PRI 분석의 방법 중 통계적인 기법과 히스토그램을 통한 기법에 대해 알아본다.
PRI Analysis 이론 및 연습
[ 통계적 기법 ]
TOA 시퀀스는 히스토그램 계산과 표준편차 및 평균을 통해 분석이 가능하다.
분석가들이 결정해야 하는 핵심은 얼마나 많은 데이터를 계산에 사용할 것인지 결정하는 것이다.
평균과 표준편차와 같은 히스토그램과 통계는 데이터의 순서에 영향을 받지 않는다.
이는 통계가 PRI 변화를 분석하는 것과 같이 간격의 순서가 중요한 분석에는 적합하지 않다는 의미이다.
예를 들면, PRI drift를 분석하기 위해서 서로 분리된 시간에 존재하는 여러 세그먼트들에 대한 PRI 평균이 계산되어야 한다.
히스토그램은 PRI 시퀀스의 전반적인 통계를 보여주는데 유용하다.
히스토그램은 예상되는 파라미터 범위를 bin으로 불리는 간격으로 나눔으로써 얻을 수 있다.
이후 각 bin 내에서 파라미터 값이 발생하는 숫자를 셀 수 있다.
랜덤 프로세스의 경우에 bin의 크기는 0에 가깝고 샘플의 수는 무한대로 가기 때문에 히스토그램은 랜덤 프로세스의 확률 분포에 가까워진다.
만약 샘플의 수가 매우 커지고 bin 크기가 고정된다면, 특정 bin에서의 히스토그램의 레벨은 이 bin에 포함되어 있는 파라미터 범위에 대한 확률 밀도 함수의 적분에 비례한다.
활용 가능한 데이터와 bin 크기 간에는 섬세한 균형이 필요하다.
만약 bin의 크기가 너무 작다면, bin에 발생할 수 있는 평균 숫자가 매우 적고 히스토그램은 비어있는 bin들과 하나 또는 두 개의 숫자만 포함된 bin들로 구성된다.
이러한 히스토그램은 분석가들에겐 불필요하다.
마찬가지로 bin 크기가 너무 크다면 모든 데이터 샘플은 하나 아니면 두 개의 bin에 모두 들어가게 되고 분석가들은 확률 분포의 모양을 알아낼 수 없게 된다.
보통의 상황은 서로 다른 bin의 크기를 갖는 여러 개의 히스토그램이 생성된다.
이후 분석가들은 데이터 활용의 품질과 양에 관해 어느 bin의 크기가 가장 적절한지 결정하게 된다.
아래의 그림은 bin 마다 많은 포인트들이 있는 히스토그램을 보여준다.
여기서 펄스의 수를 10배 그리고 100배 줄였을 때의 영향은 아래의 그림들에서 확인할 수 있다.
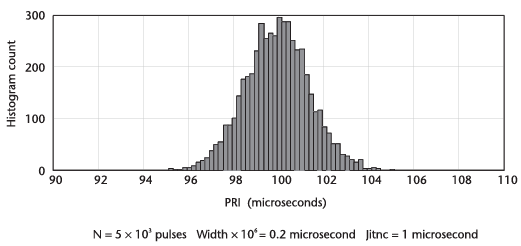
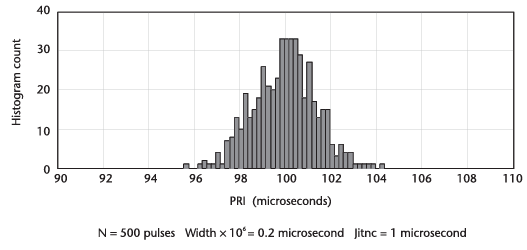
데이터가 제한적일 때, 더 넓어진 bin은 신뢰성을 향상시키지만 다음의 그림처럼 해상도에서는 손해가 발생한다.
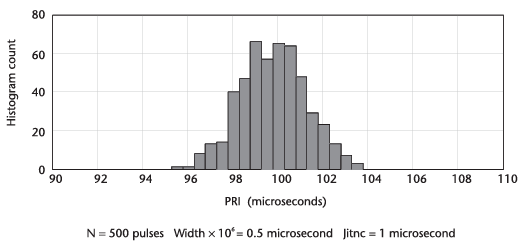
정현파 jitter가 더해진 PRI와 적은 랜덤 jitter의 히스토그램은 다음의 그림과 같다.
그리고 다음의 그림들은 펄스의 숫자가 1/10과 1/100 일때의 그림을 나타낸다.
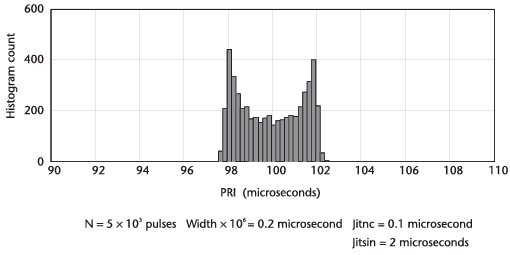
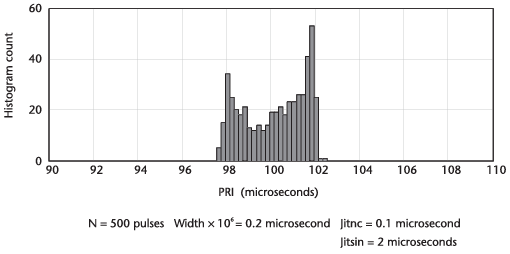
다음의 그림은 sliding PRI의 히스토그램을 나타낸다.
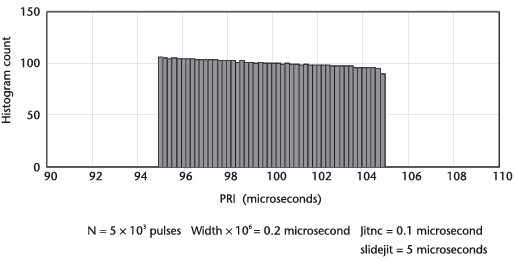
그림을 보면 상부가 평평하지 않음을 알 수 있다.
이는 더 짧은 PRI 값에서 초당 펄스의 값들이 더 긴 PRI 값들에서보다 많이 존재하기 때문이다.
따라서 고정된 저장 시간 동안 더 짧은 PRI 값들이 더 긴 PRI 값들보다 많이 저장된다.
다음의 그림은 100 ns의 랜덤 jitter를 더했을때의 영향성을 나타낸다.
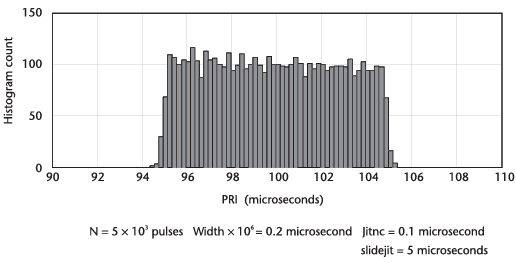
이는 히스토그램의 경사를 방해한다.
그리고 다음의 그림은 여기서 10배 많은 데이터가 랜덤 jitter가 더해졌음에도 불구하고 히스토그램의 경사를 보여주는데 얼마의 도움을 주는지 보여준다.
아래의 테이블은 공통적인 PRI 변화에 대한 히스토그램의 모양을 정리한 것이다.
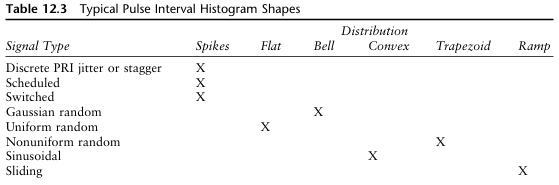
[ Delta-T 히스토그램 ]
Detla-T 히스토그램은 모든 펄스 짝들 간의 간격을 고려해서 얻은 펄스 간격들의 히스토그램이다.
다시 말해서 펄스 1과 펄스 2,3,4,등등 간의 간격을 고려하고 이후 펄스 2와 펄스 3,4,5, 등등 간의 간격을 고려하는 것이다.
전체 간격의 수는 N개의 펄스 세트에서 펄스 짝들 간의 수로 주어진다.
만약 잡음이나 간섭 펄스들의 영향성이 고려된다면 이 delta-T 히스토그램의 가치는 더욱 명확해진다.
모든 펄스 짝들 간의 시간을 검사함으로써 실제 PRI가 찾아지고 이러한 간격의 값들은 히스토그램의 피크 값에서 누적될 것이며 반면에 다른 펄스의 짝들은 히스토그램 bin들에 걸쳐 분산될 것이다.
형식적으로 delta-T 히스토그램은 펄스 TOA에 위치해있는 impulse들로 구성된 함수의 autocorrelation 한 각 히스토그램 bin들의 누적과 같은 모습을 보인다.
Autocorrelation 함수로서 delta-T 히스토그램은 주기성을 강조한다.
다음의 그림은 세 position의 stagger 그림을 보여주며 간격은 95 us, 100 us 그리고 105 us이다.
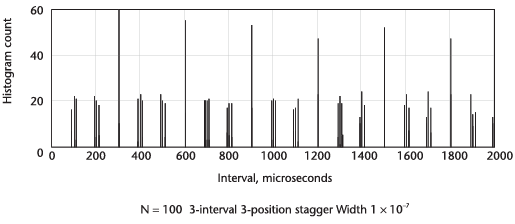
Stagger 신호에서 Delta-T 히스토그램의 피크는 stable sum이라 불리는 곳에서 발생한다.
주변의 PRI가 더해지면 결국 stagger의 주기에 도달하게 되며 어디에서 펄스의 합산이 시작되었는지는 중요하지 않다.
즉, 추가된 인접한 PRI들의 개수가 stagger 시퀀스 내에서의 position의 수와 같아질 때 stable sum이 이뤄진다.
이 stable sum과 간격의 수, 그리고 position은 레이다 위협을 식별하는 데 사용되기 때문에 ELINT 분석가들이 정확한 stagger의 주기와 시퀀스를 알아내는 것은 중요하다.
Delta-T 히스토그램은 interleaved 된 펄스 열을 분석하는 데에도 도움을 준다.
거의 동일한 두 개의 PRI 신호가 있다고 가정해 보자.
간격이 한 펄스 열에서 시작하고 다른 펄스 열의 끝에서 끝난다면 이 간격은 어느 정도 랜덤한 형태이다.
반면에 간격이 같은 펄스 열의 시작과 끝이라면 간격은 실제 한 PRI의 배수가 된다.
다음의 그림은 5 us (rms)의 noncumulative jitter와 각 100 us 및 110 us의 평균 PRI를 갖는 두 개의 에미터로부터 interleaved 펄스의 히스토그램을 나타낸다.
이는 많은 ELINT 분석가들에게 머리 아픈 퍼즐과 같은 상황을 준다.
히스토그램의 bin 크기는 1 us이다.
그림 왼쪽의 짧은 간격들은 잡음 간격들이며 한 펄스 열의 펄스에서 시작한 직후 다른 펄스 열의 끝에서 끝난 간격들로 구성된다.
100에서 110 us 근처의 구간에서 큰 피크를 볼 수 있는데 이는 두 개의 실제 PRI의 jitter 값을 나타낸다.
두 개의 피크 대신에 하나의 피크만을 보이는 이유는 두 PRI의 평균이 jitter에 2를 곱한 것만큼만 분리되기 때문이다.
200에서 220 us 구간 근처에서 또 다른 하나의 피크를 볼 수 있으며 PRI의 두 배 값을 나타낸다.
300에서 330 us 구간에서 두 개의 피크처럼 보이는 것을 알 수 있다.
400에서 440 us 구간 근처에서는 확실한 두 개의 피크가 있다.
이를 통해 두 개의 펄스 열이 존재한다는 결론을 내릴 수 있다.
게다가 평균 PRI는 네 번째 피크의 위치를 4로 나눔으로써 알아낼 수 있다.
이는 다중의 간격들의 지터는 추가되는 간격 수의 제곱근 이상으로 빠르게 증가하지 않으며 피크는 추가되는 간격의 비례하여 분리된다는 것을 말해준다.
만약 한 개의 신호가 있고 SNR이 높다면 delta-T 히스토그램은 일반적인 히스토그램이나 PRI 대 시간을 보여주는 많은 시간 도메인의 디스플레이에 비해 장점이 있다고 말할 수 없다.
하나 이상의 신호가 존재하거나 많은 잡음 펄스가 있는 조건에서 delta-T 히스토그램은 그 가치가 있다고 할 수 있다.
다음은 PRI 분석 결과와 실제 레이다에서의 응용에 대해 알아보겠다.
출처 : ELINT - The Intercept and Analysis of Radar Signals
'Electronic Warfare > EW Technology' 카테고리의 다른 글
| Pulse Repetition Interval Analysis - (4) (1) | 2025.05.01 |
|---|---|
| Pulse Repetition Interval Analysis - (3) (3) | 2025.04.28 |
| Pulse Repetition Interval Analysis - (2) (1) | 2025.04.27 |
| Pulse Repetition Interval Analysis -(1) (1) | 2025.04.13 |
| Probability of Intercept (0) | 2025.04.04 |
댓글